Recently there has been considerable interest in Pulse Forming Networks (PFN’s) as a critical component to drive high-power microwave systems and other high-energy applications requiring a relatively flat-top pulse. As a designer and manufacturer of pulsed power systems and components, APELC is very familiar with the design, construction and application of PFN’s. We would like to share some of that knowledge in the following article to help our customers better understand this incredibly useful technology.
WHAT IS A PFN?
Generally speaking, a pulse-forming network is a means of storing the amount of energy required to generate a single pulse of a specific shape by approximating the distributed inductance and capacitance of a transmission line. Either capacitors or inductors can be used to store the energy, and the elements of the network are tuned to produce the desired waveform. In the simplest sense, a transmission line or pulse-forming line (PFL) has a characteristic impedance defined by its dimensionally-defined values of inductance and capacitance, with the capacitance determined by the dielectric between the conductors (Figure 1).

Figure 1 Parallel plate vs. lumped element approximation of a transmission line

Characteristic impedance of a transmission line based upon distributed inductance and capacitance

Where is the permittivity of the dielectric, A is the area of the plates, and d is the distance between them.
The electrical length of the line is determined by the physical length and the dielectric constant, and the pulse width generated by a switched transmission line is twice that (or the two-way transit time). A handy rule of thumb is that electrical length is 1ns/ft with a dielectric constant of 1 (air), and therefore the electrical length increases as the dielectric constant increases.

Where is the velocity of propagation, is the permittivity of the dielectric and c is the speed of light
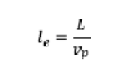
Where is the electrical length, is the velocity of propagation and is the physical length
In most pulsed power applications, the PFN is used as a means of approximating a transmission line where pulse widths are greater than several tens of nanoseconds, and the PFL would be physically excessive in length. For example- based upon the above equations, to generate a pulse width of 200ns, the PFL would need to be over 20m (67 ft) if a conventional plastic or oil dielectric ( of 2.2). Instead of a distributed transmission line filled with a dielectric, the PFN uses lumped elements (Inductors and Capacitors) to approximate a transmission line (Figure 1). The resulting circuit can be much more compact, and in some instances, even integrated into the Marx generator circuit.
WHAT ARE PFN’s USED FOR?
Many high-energy applications require a flat-top pulse to ensure energy remains constant over the duration of the pulse. This is especially useful when a specific energy photon or electron is desired over some time interval. Examples of this could be a high-power microwave (HPM) devices, such as a magnetron, where energy outside of what is useful to produce an in-band photon is wasted as heat. The same would be true in a flash-lamp (for laser or photography) where the energy distribution must remain constant to ensure a uniform spectrum. Similarly, any application where an e-beam is generated and required to have a specific energy could use a PFN. Example would include a flash x-ray tube where a flat-top pulse ensures the bremsstrahlung x-ray energy (in electron-volts) is constant to increase the fidelity of the resultant image. Another example would be a PFN used to drive the kicker magnets which steer the electron beam on a large linear accelerator system such as that shown in Figure 2. In this application the voltage on the kicker coil must remain constant to ensure the beam maintains a constant and precise deflection for a period of time.

Figure 2 Prototype of the SPS pulse-forming network at CERN. Source: CERN
WHAT IS THE THEORY BEHIND PFN’s?
The fundamental principle behind a PFN lies in the fact that a square pulse contains a number of frequency components that can be defined using Fourier analysis. These components/harmonics can be generated by individual LC circuit elements and combined to effectively “build” the square pulse. The more components, or stages of the PFN, the better the PFN can approximate a truly square pulse.

Figure 3 Harmonics contained within a square pulse

Figure 4 Fourier expansion demonstrating the increase in pulse fidelity with number of harmonics
Through this theory, a number of different circuit topologies are possible that can create a square pulse. These are referred to as Guilleman Pulse Forming Networks.


Figure 5 Types of Guilleman Networks
HOW DOES APELC APPLY PFN’s?
While APELC has the capability to build stand-alone PFN’s that can condition the output of a standard Marx Generator, our specialty is integrating the PFN into the Marx topology. A type A PFN (Figure 5) very closely resembles an erected Marx circuit. By working with the width of the buss-work between capacitors, APELC is able to tune the inductance to create a desired pulse-width and source impedance. We do this through a combination of modeling and experimentation- i.e. we utilize a finite-element code to determine a starting point for the buss-width and then construct and test an individual stage using the simulation results as a starting point for the mechanical specifications. The stage is then fired into a known load to determine impedance characteristics. Once we have established the correct dimensions for each stage, the entire Marx can then be constructed with a high-degree of confidence in meeting both pulse-width, source impedance and ripple. Two recent examples of APELC PFN Marxes are highlighted below.
MG24-20C-2700PF-PFN

Figure 6 MG24-20C-2700PF-PFN Dimensioned drawing
The APELC MG24-20C-2700PF-PFN Marx Generator was designed to drive both single and dual-tube HPM test-beds. The 24-stage PFN is designed to drive relatively high-impedance microwave tubes. The system is built into a robust stainless-steel housing/oil-tank and includes integrated diagnostics for the measurement of voltage and current. A summary of the generator characteristics and waveform are given below.
CHARACTERISTICS
- Maximum open-circuit voltage: 840 kV
- Maximum peak voltage into matched load: 420 kV
- FWHM: 260 ns
- Ripple: ± 10%
- Voltage rise time: 70 ns (10-90%)
- Energy per pulse: 20 J (at 8 kV charge) – 800 J (at 35 kV charge)
- Maximum repetition rate: 30 Hz
- Maximum number of pulses in burst: 10

Figure 7 MG24-20C-2700PF-PFN Output onto a 100 Ohm load
MG18-9C-2600PF-PFN

Figure 8 MG18-9C-2600PF-PFN Dimensioned drawing
Whereas the MG24-20C-2700PF-PFN is meant for use as a versatile test-platform requiring less portability, the MG18-9C-2600PF-PFN was designed for deployable HPM systems, such as those used in counter UAV/UAS applications. While the ripple is not as good as the MG24’s pulse, the compact, rugged, coaxial form-factor make at ideal for use on HPM systems where the source must be vehicle-mounted and rapidly moved on a guidance system to target potential threats. With a ~50 Ohm impedance, the MG18-9C-2600PF-PFN is also designed to drive lower impedance HPM loads. A summary of the generator characteristics and waveform are given below.
CHARACTERISTICS
- Maximum open-circuit voltage: 900 kV
- Maximum peak voltage into matched load: 450 kV
- Pulse rise-time: ~10ns
- FWHM: 150ns
- Maximum repetition rate: 20 Hz
- Energy per pulse: 526 J

Figure 9 MG18-9C-2600PF-PFN Output onto a 40 Ohm load
CONCLUSION
PFN’s are incredibly useful tools for converting the double-exponential output of a Marx or capacitive discharge into a flat-top/rectangular pulse for use in applications requiring a fairly constant voltage across the duration of the pulse. APELC has tailored our specialized knowledge of Marx Generators to develop Marx-PFN hybrids capable of sourcing HPM and other loads requiring a relatively rectangular pulse. The two examples given demonstrate the trade-offs between versatility in a testing environment and portability in a deployed environment. As can be seen in both examples, the waveform does not produce an ideal rectangular pulse compared to what is shown in Figure 7. This is due stage-to-stage coupling within the Marx generator. The more compact the system, the worse the ripple becomes. Beyond these examples, APELC is capable of designing and building PFN’s and PFN-Marx Generators to meet custom requirements.

